Because of the statistical nature of radioactive decay, repeated counting of an undisturbed source in a counting assembly will yield count-rate values in accordance with the frequency of a normal distribution. Deviations in these values from the normal distribution conform to the
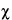 2
2 test. For this reason, the
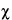 2
2 test is frequently applied to determine the performance and correct operation of a counting assembly. In the selection of instruments and conditions for assay of radioactive sources, the figure of merit
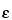 2
2/
B should be maximized (where
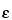
= counter efficiency = observed count rate/sample disintegration rate, and
B = background count rate).